Port-Hamiltonsche Systeme — ein modernes Paradigma zur Modellierung, Simulation, Optimierung und Regelung dynamischer Prozesse
Was beeinflusst die Dynamik?
Diese Frage lässt sich z. B. durch einen Blick auf die Energiebilanzen beantworten. Die Energieabgabe an die Umgebung oder die Energieflüsse zwischen verschiedenen Systemkomponenten sind von entscheidender Bedeutung. Aus solchen Betrachtungen ergeben sich sogenannte port-Hamiltonsche Systeme. Dabei handelt es sich um stark strukturierte Systeme von Differentialgleichungen mit zahlreichen vorteilhaften Eigenschaften. Beispielsweise
- sind port-Hamiltonsche Systeme automatisch stabil und passiv;
- die Kopplung mehrerer port-Hamiltonscher Systeme führt zu einem port-Hamiltonschen Gesamtsystem;
- verschiedene Bereiche der Physik (z. B. Elektrodynamik, Mechanik) können leicht miteinander kombiniert werden, was eine einheitliche Behandlung von Multiphysiksystemen ermöglicht.
Neben der Analyse der Eigenschaften derartiger Systeme spielt die Entwicklung von Simulations-, Optimierungs- und Regelungsalgorithmen, die die Struktur ausnutzen oder erhalten, eine sehr wichtige Rolle in der Forschung. Diese Themen werden aktuell auch an der FernUni Schweiz verfolgt.
Systeme verkleinern, um sie besser zu verstehen
Port-Hamiltonsche Systeme, die in der Praxis vorkommen, werden oft durch eine sehr grosse Variablenzahl beschrieben und sind damit sehr komplex, sodass die Simulation, Optimierung und Regelung äusserst zeitaufwändig sind. Daher ist es notwendig, den dominierenden Teil der Dynamik mithilfe automatisierter Modellreduktionsmethoden zu extrahieren, um so ein reduziertes port-Hamiltonsches System mit einer sehr geringen Anzahl an beschreibenden Variablen zu erhalten. Dies kann z. B. durch einen datenbasierten Ansatz erreicht werden, bei dem die Reaktion des Systems auf Anregungen mit unterschiedlichen Frequenzen berechnet oder gemessen wird. Dies führt zu einer neuen Art von Methoden zur Modellreduktion, die auf der Optimierung und der Anpassung von Daten an ein dynamisches System mit gegebener Struktur und Dimension beruhen.
Insbesondere konnte gezeigt werden, dass bei gleicher reduzierter Systemdimension deutlich genauere reduzierte Modelle erzielt werden können als mit bekannten strukturerhaltenden Modellreduktionsverfahren.
Entwicklung von Reglern
Ein weiterer Schwerpunkt ist die Entwicklung von Reglern für port-Hamiltonsche Systeme, um beispielsweise mit Hilfe von Messdaten im Betrieb ein gewünschtes Systemverhalten zu erreichen. Eine Kategorie von Reglern sind sogenannte H-unendlich-Regler, deren Ziel es ist, das geregelte System möglichst unempfindlich gegenüber äusseren, nicht messbaren Störeinflüssen und Messfehlern zu machen. Bei port-Hamiltonschen Systemen kann man die Struktur ausnutzen und dieses Ziel durch Kopplung mit einem port-Hamiltonschen Regler erreichen, sodass das gekoppelte System allein schon aufgrund seiner Struktur bestimmte Stabilitätseigenschaften besitzt. Die entsprechenden Ergebnisse zeigen eine ähnliche Egebnisqualität im Vergleich zu anderen etablierten Algorithmen, jedoch zeigt der neue Ansatz auch vielversprechende Eigenschaften für die Behandlung höherdimensionaler Problemen auf. In diesem Zusammenhang ist auch geplant, die Behandlung zusätzlicher Modellunsicherheiten im Reglerentwurfsverfahren zu integrieren.
Gibt es weitere potenzielle Untersuchungsansätze?
In diesem Bereich gibt es noch viele offene Fragen. Beispielsweise könnten reduzierte Modelle auch durch Systemsimulationen in Kombination mit Methoden des maschinellen Lernens bestimmt werden. Dies würde z. B. die Behandlung nichtlinearer Dynamiken oder die Integration stochastischer Grössen umfassen. Eine weitere Forschungsrichtung besteht in der Datenassimilation port-Hamiltonscher Systeme, d. h., der Aktualisierung des reduzierten Systems während des realen Prozesses durch gemessene Daten. Dies würde es beispielsweise ermöglichen, modellbasiert genauere Steuersignale während der Prozessdauer zu berechnen.
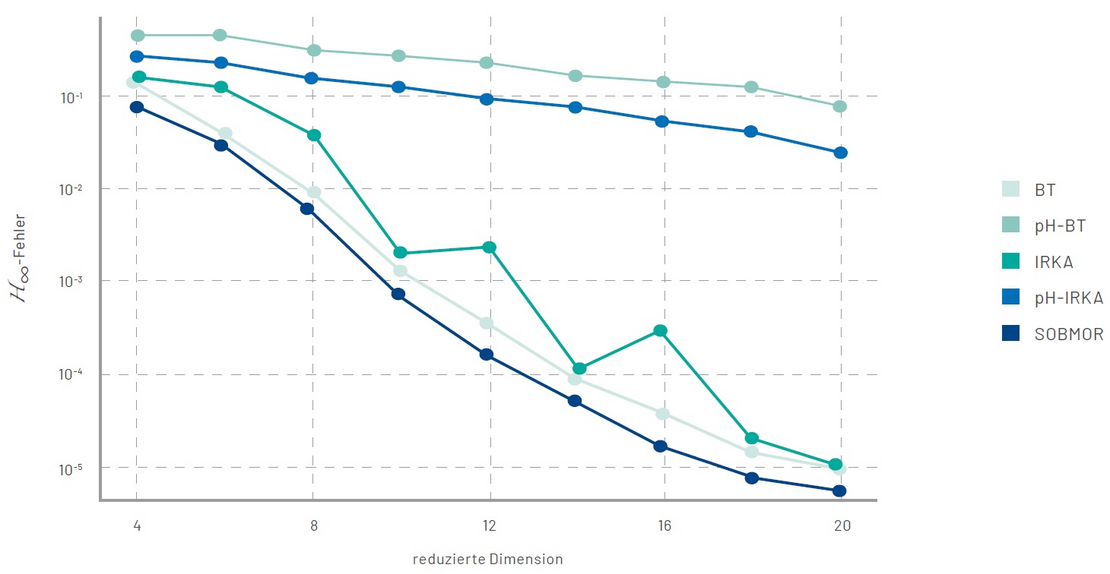
Vergleich des neuen Ansatzes (SOBMOR) mit anderen strukturerhaltenden Modellreduktionsverfahren (pH-BT, pH-IRKA) und generischen Verfahren (BT, IRKA)
Matthias Voigt

Prof. Dr. Matthias Voigt ist Assistenzprofessor an der Fakultät Mathematik und Informatik und unterrichtet im Rahmen des Bachelor-Studiengangs in Mathematik.
Seine Forschungsgruppe beschäftigt sich hauptsächlich mit Fragestellungen der mathematischen Systemtheorie, insbesondere mit der Entwicklung von automatisierten Verfahren zur Komplexitätsreduktion dynamischer Systeme.
Prof. Dr. Matthias Voigt hat in Zusammenarbeit mit Prof. Dr. Thomas Mettler eine Vortragsreihe (UniDistance Suisse Mathematics Colloquium) lanciert, um die Fakultät Mathematik und Informatik bekannter zu machen. Das Mathematik-Kolloquium richtet sich an ein spezifisches Fachpublikum.
Weitere News

Assistant-e pour le module Psychopathologie du bachelor en psychologie (80% / 50%)
FernUni Schweiz Weiterlesen
Lehrbeauftragte oder Lehrbeauftragter für das Modul «M07 Persönlichkeit und Differentielle Psychologie, 10 ECTS» (18%) (copie 1)
FernUni Schweiz Weiterlesen


